程序填空题:欧几里德法求最大公约数 - 实验9 循环进阶 - 《Python编程实验》
两个正整数的最大公约数(Greatest Common Divisor)是指两个正整数的公有约数中最大的一个。即如果GCD(x,y) = k,则k是能同时整除x和y的最大除数。<br><br>
欧几里德(Euclidean)在《几何原本》中描述了一种求解最大公约数的快速算法,即辗转相除法。其数学表达式为:<br><br>
GCD(x,y) = GCD(x, x % y ) 设x >= y
<br><br>
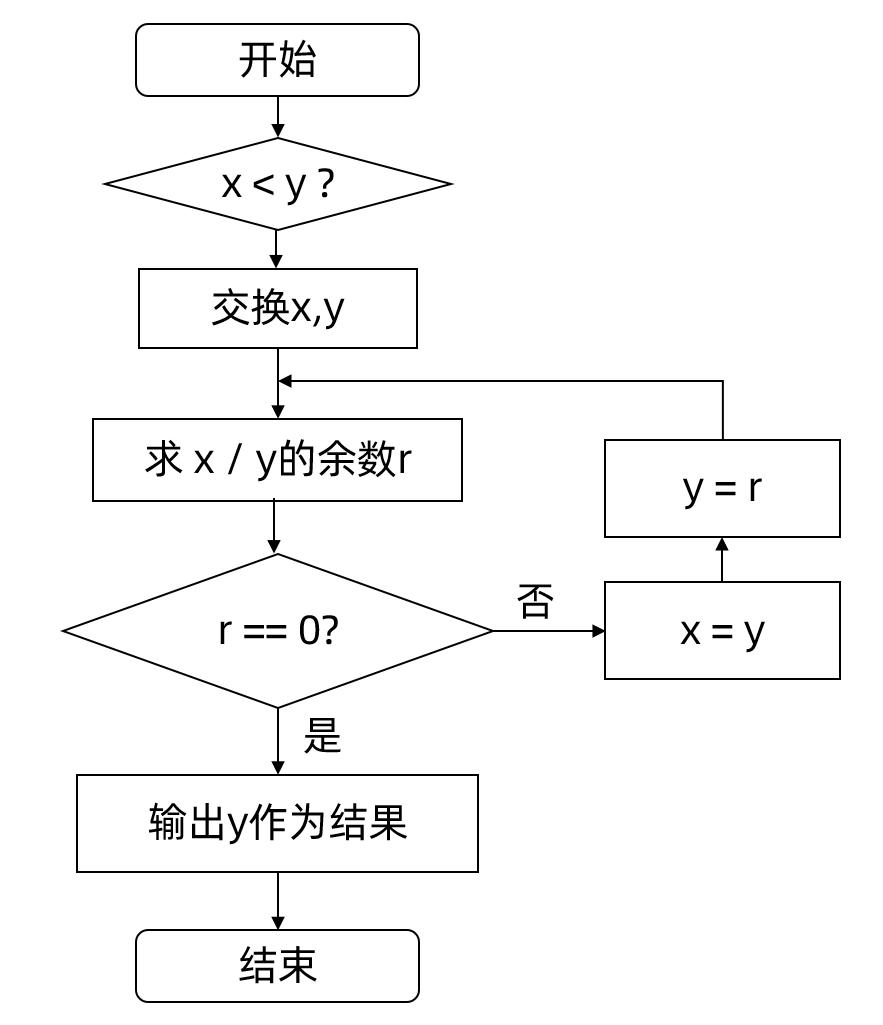
请结合上述流程图,使用完成程序填空,将上机调试运行。<br><br>
python
x = eval(input("请输入整数x:"))
y = eval(input("请输入整数y:"))
if x < y:
while True:
r =
if r==0:
x = y
print("GCD(x,y) =",y)
<br>
解题思路: 请参考《Python编程实验》(待出版)。<br> 该书是高等教育出版社《Python编程基础及应用》教材的配套实验指导书。
答案:
第1空:x,y = y,x
第2空:x % y
第3空:break
第4空:y = r
欧几里德(Euclidean)在《几何原本》中描述了一种求解最大公约数的快速算法,即辗转相除法。其数学表达式为:<br><br>
GCD(x,y) = GCD(x, x % y ) 设x >= y
<br><br>

请结合上述流程图,使用完成程序填空,将上机调试运行。<br><br>
python
x = eval(input("请输入整数x:"))
y = eval(input("请输入整数y:"))
if x < y:
while True:
r =
if r==0:
x = y
print("GCD(x,y) =",y)
<br>
解题思路: 请参考《Python编程实验》(待出版)。<br> 该书是高等教育出版社《Python编程基础及应用》教材的配套实验指导书。
答案:
第1空:x,y = y,x
第2空:x % y
第3空:break
第4空:y = r