计算智能题库 约束多目标优化算法
第十章 约束多目标优化算法 习题与答案
1. 填空题
(1)在约束优化问题中, 的存在导致搜索空间的拓扑结构变得十分复杂,可行域空间将变得不连通,需要算法较好地协调 搜索和 搜索。当所求问题存在多个不连通的可行域时,将会有多个局部最优解,要求算法兼顾良好的 和 。
(2)为了判断已知解是否满足约束条件,对约束条件不满足的程度,定义了 函数。其值越大,说明已知解不满足约束条件的程度 。变量空间中所有解构成的集合其中包括 解和 解。
解释:
本题考查约束多目标优化算法的基础知识。
具体内容请参考课堂视频“第10章约束优化算法”及其课件。
答案:
(1)约束条件,全局,局部,多样性,收敛性
(2)约束违反度,越大,可行,不可行
2. 简述约束违反度含义。
解释:
本题考查约束违反度含义。
内容请参考课堂视频“第10章约束优化算法”及其课件。
答案:
约束违反度是衡量不满足约束条件时对约束条件不满足的程度,即 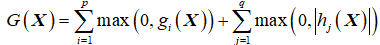 。约束违反度越大,说明已知解不满足约束条件的程度越大;约束违反度越小,说明已知解不满足约束条件的程度越小。
。约束违反度越大,说明已知解不满足约束条件的程度越大;约束违反度越小,说明已知解不满足约束条件的程度越小。
3.简要介绍约束处理技术,并说明它们的特点。
解释:
本题考查常见的约束处理技术。
内容请参考课堂视频“第10章约束优化算法”及其课件
答案:
(1)惩罚函数法通过对目标函数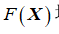 增加惩罚项
增加惩罚项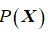 来构造惩罚适应度函数
来构造惩罚适应度函数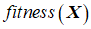 ,由于惩罚函数法因为参数难以选择,目前已几乎不再使用。
,由于惩罚函数法因为参数难以选择,目前已几乎不再使用。
(2)随机排序法采用随机概率对目标函数值或约束违反度进行个体比较,与惩罚函数法同样缺点,随机概率值不易确定。
(3)Deb准则中可行解的比较采用Pareto支配关系,可行解优于不可行解,约束违反度小的不可行解占优,由于强调可行解一定优于不可行解,极易陷入局部收敛。
(4)ε约束法是对Deb准则的一种改进,主要改进之处在于通过设置水平参数ε将种群中约束违反度小于ε的不可行解当作可行解,进而让这些不可行解有机会参与进化,以加强对可行域边界的探索力度。多目标优化法是将约束条件转化成目标函数,利用多目标优化技术对这一多目标优化问题求解,计算复杂度增加。
(5)双种群存储技术利用可行解集和不可行解集分别存储可行解和不可行解,来避免两者的直接比较,由于只考虑利用约束违反度来更新不可行解,导致目标值较差的不可行解保留下来,进而影响种群的收敛性,并且双种群存储技术忽略了可行解和不可行解的信息交流和协同进化,算法效率受到了限制。
4.试说明Deb准则和ε约束的区别和联系,及各自的优缺点。
解释:
本题考查两种约束处理技术的核心思想。
内容请参考课堂视频“第10章约束优化算法”及其课件。
答案:
Deb准则主要由三条准则构成:(1)两个待比较的个体都是可行解时,目标函数值较小的个体获胜;(2)两个待比较的个体一个是可行解另一个是不可行解时,可行解获胜;(3)两个待比较的个体都是不可行解时,约束违反度较小的个体获胜。
Deb准则主要有以下两个优点:(1)它强调可行解优于不可行解,能够加快进化向可行域方向进行;(2)原理简单,操作方便,无需设置额外参数,便于在实际中应用。由于Deb准则强调可行解一定优于不可行解,所以它会限定进化只在可行域内进行,使得对于可行域较小或具有多个不连通可行域的约束优化问题,算法极易陷入局部收敛。
ε约束是对Deb准则的一种改进,主要改进之处在于ε约束通过设置水平参数ε将种群中约束违反度小于ε的不可行解当作可行解,进而让这些不可行解有机会参与进化,以加强对可行域边界的探索力度。ε约束法放宽了对不可行解的限制,让部分约束违反度较小的不可行解参与进化,从而扩大算法的探索范围,提高种群多样性,从而提高了算法的收敛精度。
5. 画图分析约束违反度小的不可行解对种群进化的好处。
解释:
本题考查ε约束法的核心思想。
内容请参考课堂视频“第10章约束优化算法”及其课件。
答案:
约束违反度小的不可行解常位于可行域边界附近,对快速找到最优可行解有着很大帮助,如图所示:当可行解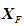 的目标函数值较差,不可行解
的目标函数值较差,不可行解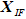 的目标函数值较优同时约束违反度较小时(如图10.3所示),此时不可行解更接近真实PF,因此保留不可行解
的目标函数值较优同时约束违反度较小时(如图10.3所示),此时不可行解更接近真实PF,因此保留不可行解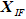 更利于搜索到更优可行解。
更利于搜索到更优可行解。
6. 简述求解约束单目标优化问题的难点所在。
解释:
本题考查约束单目标优化问题。
内容请参考课堂视频“第十章约束优化算法”及其课件。
答案:
相比于无约束单目标优化问题,约束单目标优化问题由于存在各种约束条件(等式、不等式、线性和非线性等),其可行域空间的拓扑结构将变得十分复杂。例如,当约束条件数量较多时,可行域范围将变得十分狭小,此时需要算法具有良好的多样性能力,才能搜索到全局最优解。当具有多个不连通的可行域时,将会存在多个局部最优解,此时需要算法具备较强的探索能力,穿越不同的可行域进行充分搜索,从而保证种群最终逼近到全局最优解。
7. 简述双种群存储求解约束单目标优化问题时双种群的更新方法。
解释:
本题考查基于双种群存储的约束单目标优化算法。
内容请参考课堂视频“第10章约束优化算法”及其课件。
答案:
首先是不可行解集的更新:将上一代不可行解集与当代不可行解集合并,选取非劣不可行解。如果非劣不可行解的数量小于等于不可行解集的预定规模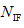 ,将其作为下一代不可行解集。如果非劣不可行解的数量大于
,将其作为下一代不可行解集。如果非劣不可行解的数量大于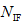 ,则选取约束违反度最小的
,则选取约束违反度最小的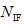 个体。其次是可行解集的更新:进化初期由于可行解的数量可能比较少,为快速产生
个体。其次是可行解集的更新:进化初期由于可行解的数量可能比较少,为快速产生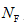 个(可行解集的预定规模)可行解,利用Deb准则比较个体,同时将上一代可行解集与当代可行解集合并,从中选取目标函数值最优的
个(可行解集的预定规模)可行解,利用Deb准则比较个体,同时将上一代可行解集与当代可行解集合并,从中选取目标函数值最优的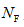 个体作为下一代可行解集。
个体作为下一代可行解集。
8. 简述求解约束多目标优化问题的难点所在。
解释:
本题考查约束多目标优化算法。
内容请参考课堂视频“第10章约束优化算法”及其课件。
答案:
相较于约束单目标优化问题,约束多目标优化问题由于目标数量的增多,多个目标之间往往相互冲突,提高某个目标的性能可能会降低其他目标的性能,必须利用协调和折中的方法让所有目标尽可能达到最优,并且所求是一组互不支配的Pareto最优解。因此,约束多目标优化问题要求算法在最优可行区域内保证解集的收敛性和分布性,需要算法在可行性,收敛性和多样性三者之间保持平衡。如何在求解问题特性未知的情况下,设计一种自适应平衡技术在求解约束多目标优化问题的过程中动态平衡三者,是求解约束多目标优化问题的难点所在。