主观题:旅行商问题
给定一个n顶点网络(有向或者无向),找出一个包含n个顶点且具有最小耗费的环路。任何一个包含网络所有顶点的环路成为一个旅行。旅行商问题是要寻找一条耗费最小的旅行。
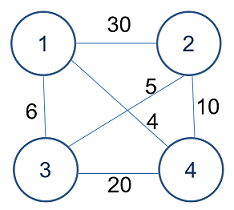
请问:
(1)旅行商问题可以用哪种算法来解决?(2分)
(2)请描述所选择的算法的思想。(5分)
(3)请写出该算法解决上图旅行商问题的过程。(5分)
(4)给出上图中从1出发的一条耗费最小的旅行。(3分)
answer:评分点 1:回溯法或动态规划法或分支定界法或贪心算法(2 分)。
评分点 2:回答出任意一种都可以(5分)
(1)如果回答回溯法,则解释回溯法。回溯法是搜索问题解的一种系统方法。
(2)如果回答动态规划法,则解释动态规划法。动态规划算法要考虑一系列的抉择,以确定一个最优抉择序列是否包含最优抉择子序列。
(3)如果回答分支定界法,则解释分支定界法。该算法是搜索问题解的一种系统方法。
(4)如果回答贪心算法,则解释贪心算法。每次在选取时,选取两地之间费用最少的路径,选取局部最优解,直到所有的路径可以构成环路,同时因为每次选取局部最优解,最终局部最优解构成全局最优解。
评分点 3:
(1)如果回答回溯法,则步骤是:第一步是定义问题的解空间;第二步是组织解空间;第三步是按照深度优先搜索的方式搜索解空间(5分)。
(2)如果回答动态规划法,则步骤是:第一步证实最优原则是适用的;第二步建立动态规划的递归方程式;第三步求解动态规划的递归方程式以获得最优解;第四步沿着最优解的过程进行回溯。
(3)如果回答分支定界法,则步骤是首先定义解空间,然后组织解空间,用广度优先方式搜索解空间,最后依据最小耗费或最大收入求解。
(4)如果回答贪心算法,则步骤是首先选取费用最少的两个点,即①和④,此时①和④两点包括到了路径中,但是并未包括所有的点,同时并未构成环路,所以再次进行选取,选取②和③,此时所有点已经包括,但是并未构成环路,所以继续进行以上过程,直到构成环路。
评分点 4:从1出发的耗费最小的旅行是 1-3-2-4-1或1-4-2-3-1(3分)

请问:
(1)旅行商问题可以用哪种算法来解决?(2分)
(2)请描述所选择的算法的思想。(5分)
(3)请写出该算法解决上图旅行商问题的过程。(5分)
(4)给出上图中从1出发的一条耗费最小的旅行。(3分)
answer:评分点 1:回溯法或动态规划法或分支定界法或贪心算法(2 分)。
评分点 2:回答出任意一种都可以(5分)
(1)如果回答回溯法,则解释回溯法。回溯法是搜索问题解的一种系统方法。
(2)如果回答动态规划法,则解释动态规划法。动态规划算法要考虑一系列的抉择,以确定一个最优抉择序列是否包含最优抉择子序列。
(3)如果回答分支定界法,则解释分支定界法。该算法是搜索问题解的一种系统方法。
(4)如果回答贪心算法,则解释贪心算法。每次在选取时,选取两地之间费用最少的路径,选取局部最优解,直到所有的路径可以构成环路,同时因为每次选取局部最优解,最终局部最优解构成全局最优解。
评分点 3:
(1)如果回答回溯法,则步骤是:第一步是定义问题的解空间;第二步是组织解空间;第三步是按照深度优先搜索的方式搜索解空间(5分)。
(2)如果回答动态规划法,则步骤是:第一步证实最优原则是适用的;第二步建立动态规划的递归方程式;第三步求解动态规划的递归方程式以获得最优解;第四步沿着最优解的过程进行回溯。
(3)如果回答分支定界法,则步骤是首先定义解空间,然后组织解空间,用广度优先方式搜索解空间,最后依据最小耗费或最大收入求解。
(4)如果回答贪心算法,则步骤是首先选取费用最少的两个点,即①和④,此时①和④两点包括到了路径中,但是并未包括所有的点,同时并未构成环路,所以再次进行选取,选取②和③,此时所有点已经包括,但是并未构成环路,所以继续进行以上过程,直到构成环路。
评分点 4:从1出发的耗费最小的旅行是 1-3-2-4-1或1-4-2-3-1(3分)